Foucaut Sinusoidal¶
Classification |
Pseudocylindrical |
Available forms |
Forward and inverse, spherical projection |
Defined area |
Global |
Alias |
fouc_s |
Domain |
2D |
Input type |
Geodetic coordinates |
Output type |
Projected coordinates |
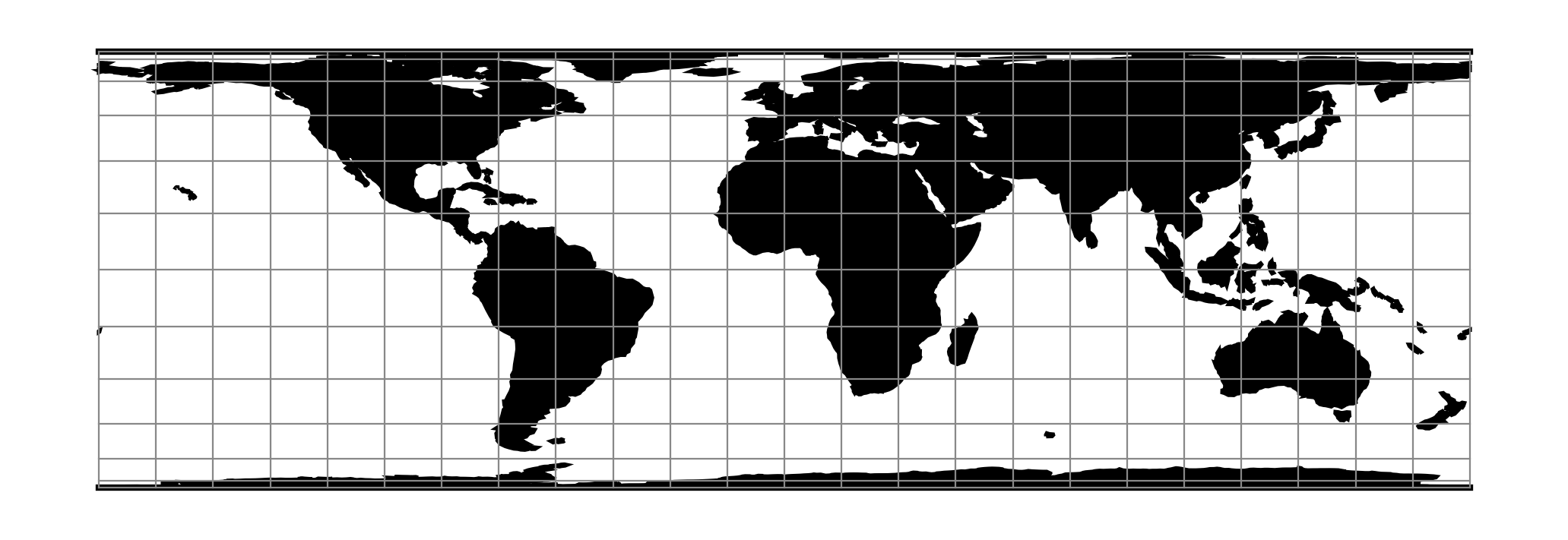
proj-string: +proj=fouc_s¶
The y-axis is based upon a weighted mean of the cylindrical equal-area and the sinusoidal projections. Parameter \(n=n\) is the weighting factor where \(0 <= n <= 1\).
For the inverse, the Newton-Raphson method can be used to determine \(\phi\) from the equation for \(y\) above. As \(n \rightarrow 0\) and \(\phi \rightarrow \pi/2\), convergence is slow but for \(n = 0\), \(\phi = \sin^1y\)
Parameters¶
Note
All parameters are optional for the Foucaut Sinusoidal projection.
- +n=<value>¶
Weighting factor. Value should be in the interval 0-1.
- +lon_0=<value>¶
Central meridian/longitude of natural origin, longitude of origin or longitude of false origin (naming and meaning depend on the projection method).
Defaults to 0.0.
Note
The default convention is to interpret this value as decimal degrees. To specify radians instead, follow the value with the "r" character.
Example: +lon_0=1.570796r
See Projection Units for more information.
- +R=<value>¶
Radius of the sphere, given in meters. If used in conjunction with
+ellps,+Rtakes precedence.See Ellipsoid size parameters for more information.
- +x_0=<value>¶
False easting, easting at false origin or easting at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.
- +y_0=<value>¶
False northing, northing at false origin or northing at projection centre (naming and meaning depend on the projection method). Always in meters.
Defaults to 0.0.